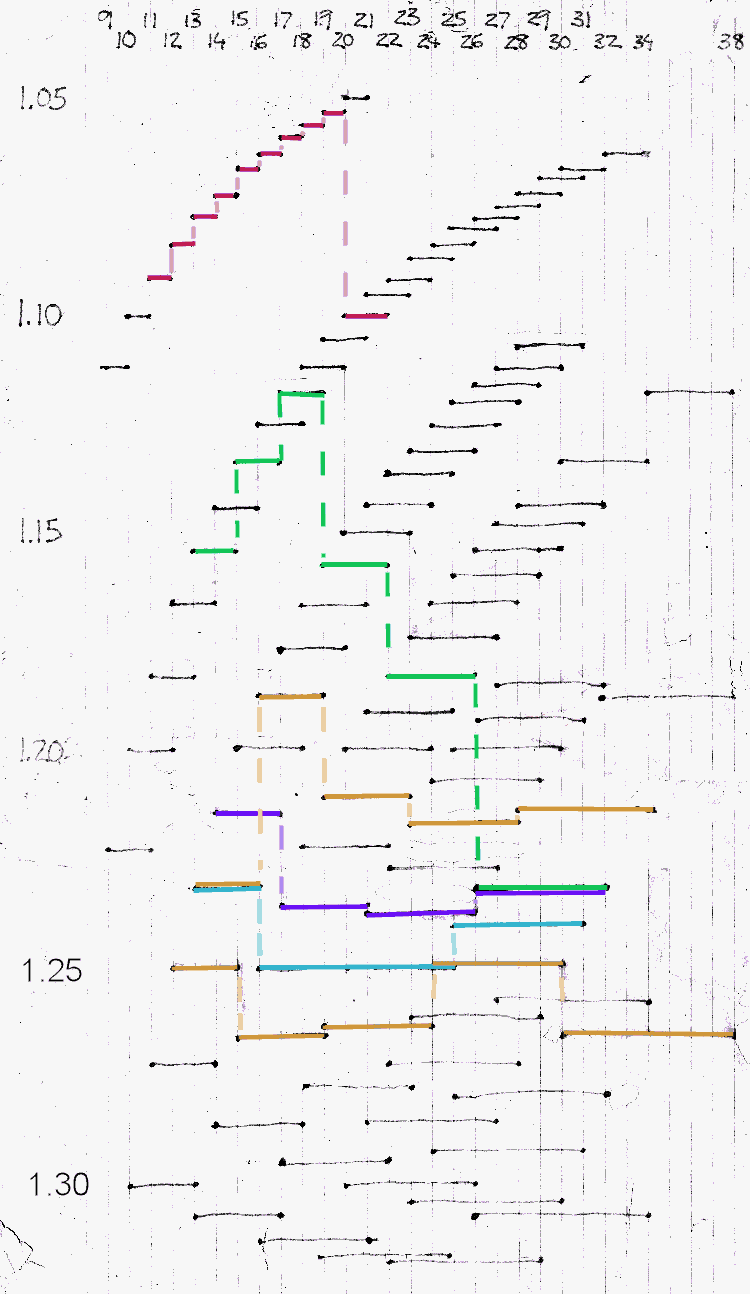
While cleaning up my home office, I found the diagram in this article, on an old, yellowed sheet of lined paper. I drew the diagram decades ago, before I had access to computer graphics. It's a bit rough looking, but it gets an idea across.

The numbers at the top of the diagram are tooth counts of bicycle sprockets. In the area below, each possible pairing of sprockets is represented by a horizontal line with a sprocket at each end. The curved sequence at the upper left is for one-tooth jumps, the next lower one for two-tooth jumps, and so forth. The numbers at the left identify ratios established by pairs of sprockets.

The point of this diagram? Plotting the sprocket pairs and ratios as a two-dimensional graph makes it possible clearly to see which pairs have nearly the same ratio -- and to identify good sequences.

On a bicycle freewheel or cassette, each sprocket (except the innermost and outermost ones) has two pairings -- one with the next smaller sprocket, one with the next larger sprocket. I have drawn colored lines to indicate some interesting combinations. The horizontal lines link sprockets in a pair, and the vertical, dashed lines show linkages of a sprocket to another smaller and another larger one. In this way, it is possible to construct the sequence for an entire cluster of sprockets. As an example, the red stair steps near the upper left represent a "corncob" cluster, with one-tooth jumps up through 20 teeth, then the descending dashed line goes to where the 20-tooth sprocket is paired with the largest one, with 22 teeth.

This representation clearly shows how the steps established by one-tooth jumps become smaller as the number of teeth increases, and that the two-tooth jump between the 20 and 22 tooth sprockets is nearly twice as great as the adjacentt one between the 19 and 20. Similarly for the other sequences illustrated with colored lines.

I'll have further explanations below the diagram...

Now let's look at more of the sequences that I have highlighted with colored lines in the diagram.

The one in green is the 7-sprocket sequence on my Cannondale road bike, 13-15-17-19-22-26-32. Notice how the steps get smaller from 13 through 19, but the 19-22 tooth jump is almost the same as the 13-15. A 31 at the bottom end would make for a more even progression than the 32, but on the other hand, I have paired this cluster with a 50-34 compact double crankset. Using all 7 sprockets with the 50-tooth chainring covers almost all my needs except for steep climbs. The double shift to the 34-tooth chainring and 26-tooth sprocket gives me a step nearly the same size at the shifts above and below. The overall range is 28 to 104 gear inches, with an easily remembered sequence and no "surprise" steps.

The remaining four sequences,

• 13-16-19-23-28-34,
• 13-16-20-25-31 (a 31 was once made by Regina in Italy; you'd have trouble finding one today.);
• 14-17-21-26-32,
• 12-15-19-24-30-38,

are intended for use in half-step plus granny systems. The steps in the sprocket cluster are large, but all nearly enough the same so they can be "half-stepped" with a pair of chainrings only a few teeth different. A half-step system with a third, small chainring for "granny" gears allows an extremely wide range and small, even steps with only 5 or 6 sprockets on an older frame with narrow rear dropout spacing. Half step used to be a pain to use with all the double shifts, but it works nicely with indexed bar-end shifters.

If I were to redo this diagram, I'd make it more illustrative by using logarithmic horizontal and vertical scales, so the same ratios appear the same size throughout. Logarithmic scales would make it possible to pair the diagram with a similar one for chainrings, adjusting that one's relative position to show double shifts. I'd add more sprockets, reflecting what is now available. I might also flip the diagram vertically so larger steps are at the top.

I hope to find someone skilled in computer graphics to create an updated version.