An Alternative Method of Bike Fit

|
HTML and additional editing by Sheldon Brown
Minor edits and a few comments by John Allen

|
Exploding myths is tough work. People don't want to believe that their ideas about how things work or how things should be are wrong. Keith Bontrager tackles one of our primary beliefs about bike fit: that aligning the rider's knee over the pedal spindle is critical for proper positioning. He shows that there is no physiological basis for it. His dismissal of that rule, and his alternative method of bike fit, is based on quite a bit of anatomical study and a lot of practical experience in fitting riders to his custom-built framesets. Some of the ideas in this article may be initially hard to grasp, but if you bear with it, you will derive an understanding of an approach to bike fit that considers the needs of the rider in all riding positions, not just the seated one.
-Doug Roosa.
![]()
I wrote this article many years ago, when I was making custom frames and studying physics. There was a motivation for this article that was not purely scientific.
The fitting method used in the Fit Kit was becoming popular when I wrote the article. It was (is?) a collection of lookup tables and some measuring devices designed to help shop staff determine the proper frame size for a given rider quickly and with confidence, a simple, packaged means of determining a custom fit that could be marketed to dealers. It was reasonable in that respect, though not much more than a slick version of the traditional Italian methods, adapted a little to work for a wider range of riders. It also had some cleat adjusting hardware that was very tricky.
The methods and procedures employed in the Fit Kit were based on tradition, some statistics, and the inventor's coaching instincts and experience. That's not unreasonable given that it is about the same as had been done for years in the sport. But, for the marketing of the kit, the Fit Kit folks had to create the impression that there was more behind it, that it was based in physiology and was physically correct somehow. Even if they didn't claim it directly, it ended up with that impression in the dealers' and consumers' minds somehow. Given that kind of authoritative clout, the process added a lot more confidence to the selling process.
This presented an interesting paradox for them as well. Dealers wanted some "flexibility" in the output, so they could select a "best fit" from a range of dimensions, large enough to find a fit from their existing stock of bikes, without looking so large that it lost the authority and credibility that was useful. They worked it out somehow - the magic of marketing.
I was building custom bikes at the time and going to school studying physics. The Fit Kit's popularity and marketing effectiveness left me in a situation where I was having to discuss and defend my own recommendations with customers who had had a Fit Kit session in a shop and who were convinced that the methods used in that process were infallible. My recommendations were based on the traditional methods at that time and my experience - we all read the same books, studied the same history and ride similar bikes. Often the disagreements were not large, but it bothered me that the marketing for their method was so effective.
It was clear to me that, based on dynamical considerations (dynamics is the study of the motion of the bicycle, and in particular, how it goes around corners), the rider's horizontal location and position on the bike could determine its handling characteristics to some extent. The KOPS method used in the Fit Kit didn't account for that. Neither did the traditional Italian method, but the range of applications that method was used for was narrow - road and track racing, so it was less important to take it into account.
And, it was also obvious that the safety frame was not evolving on a carefully executed scientific basis. The physiological efficiency of the seated rider had never been carefully optimized in a formal way, though this might have occurred over the years through the empirical methods employed by cyclists. There was a seemingly large range of possible rider positions and geometries that worked well. It led me to the supposition that the topology of the "efficiency" curves was pretty flat in the range of possibilities that were given by the traditional methods, or that riders could adapt to this range of configurations and train to use them effectively, or both. It made sense.
One thing you learn quickly as a framebuilder is that the well-designed bike and rider fit together in each riding position in a very harmonious way, with very little interference or restriction. This is, as one experiments with bike geometry, a pretty fragile relationship. There is not much one can vary from the range of accepted traditional frame geometry and rider setup without compromising the rider's effectiveness in one or more of the important pedaling positions. Given the slow, cut-and-try evolution of the safety frame and modern components, this is very likely to be significant in the traditional method, though no one has stated it clearly.
All of this prompted a study of the simple physics involved. I figured that it would be a good thing if I could offer a plausible explanation for how it works that includes some physics rather than statistics and traditions. Certainly the KOPS rule would be a fatality in the process.
The most important argument I came up with to establish a basis for believing that KOPS is only an accidental relationship, only has a weak statistical basis and is not physically significant is the discussion of the recumbent. In that case, the location of the rider's knees over the pedals is completely different, entirely unrelated to gravity, but the position is as effective in pedaling. This gives you a very simple way to see that the KOPS method has no basis in physics or physiology.
I still believe that the rest is an adequate description of the way it all works, though it could be written better. It is not very well fleshed out in some areas. I always wanted to photograph riders in the various positions and overlay a CG to explain things. I did it in a few instances, but nothing I could present. It would be more useful than the simple graphics.
This explanation will never be a commercially viable fitting technique. It is too complicated. So is the world. Simple methods like the traditional ones will be more useful.
Oh yeah...
Please don't request equations or computer algorithms for this fit technique. They are not available. I buried them in the backyard with a lot of other ideas that had merit but were too complicated to do anything with (beyond using myself for the exercise).
I think it is possible to derive them from the basics presented in the discussion. The real work is that of measuring the rider's CG accurately. I'll leave you to that as well. It's possible. Have fun with it!
KB
![]()
![]()
For the cyclist interested in performance, good bike fit is paramount. A properly fitted rider will feel efficient and comfortable on the bike. An efficient position is one that enables the rider to produce more power for a given muscular effort, and to produce that power without working any muscle groups excessively or needlessly. Comfort and efficiency may be at odds in certain riding conditions, however, so riding position may have to be modified to favor one quality over the other. In a time trial, for instance, efficiency matters most, so a position allowing the best aerodynamics is desirable. But in a long road race, an uncomfortable bike may ultimately be more fatiguing than a small loss in efficiency.
Good bike fit has three general parameters: correct saddle height, correct saddle-to-bar distance, and correct fore and aft saddle position. The established methods for finding the correct saddle height (seat tube length) and saddle-to-bar distance (top tube and stem length) seem fairly straightforward. For maximum power, the cyclist's leg should be nearly extended at the bottom of the pedal stroke (This advice is good for your knees, too; the straighter your legs are during the peak power portions of the pedal stroke - usually between 100 to 130 degrees from top dead center - the better it is for your knee joints - D.R.). The reach to the bars should allow the cyclist to assume a comfortable position whether sitting or standing.
In my opinion, the primary difficulty in finding the correct fit for a road cyclist is in determining the correct horizontal saddle position. This aspect is important because saddle position has a direct bearing on frame geometry. Saddle position affects seat tube angle as well as the top-tube/stem-length dimension.
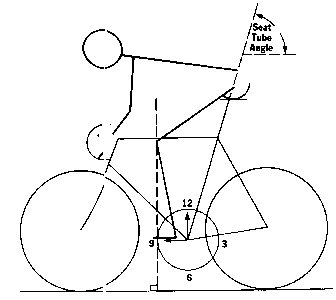
The traditional method for achieving horizontal saddle position is to position the rider's saddle so that the bump below the knee (the tibial tuberosity) is over the pedal spindle with the crank horizontal to the ground. I'll call this the "KOPS" (Knee Over the Pedal Spindle) method (see Figure 1).
The common way to check this position is with a plumb bob. Typically, a framebuilder will choose a seat tube angle that places the saddle at the center of the seatpost clamp with the rider's knee in this position.
The KOPS rule seems sensible enough; it puts the knee in line with the pedal at maximum pedaling force, which must help, right? Wrong. The KOPS rule of thumb has no biomechanical basis at all. It is, at best, a coincidental relationship that puts the rider somewhere near his or her correct position. It probably grew out of someone's observations that many successful riders sit on their bicycles with their knees somewhere over the pedal spindle. In fact, there has been little comprehensive work done in the field of cycling biomechanics that has studied rider position on the bicycle in order to maximize power input or minimize fatigue. Most builders and fitting specialists rely on customer feedback to tell them whether a change in position feels better or worse. This information doesn't pertain to power output; it is a result of physiological response called perceived exertion, only one of the several important variables that are related to a rider's muscular effort. In short, there is no scientific evidence to support the KOPS method.
The KOPS method is arbitrary because it relies on the gravitational orientation of a plumb bob. The direction of gravitational force has no bearing on the rider's ability to pedal, except for providing a constraining force at the saddle to counteract the peak portion of the pedal cycle. In analyzing the pedaling motion of a cyclist, it is not useful to think of the thigh as pushing down on the pedal through the knee. It is better to look at the rider's leg and its attachment to the pedal and crank as a system of levers and pivots, and to consider how the pedaling forces and joint torques act on this system.
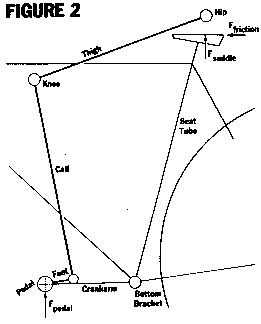
Consider the lever system made up of the rider's leg, pedal crank, and bottom bracket drawn in Figure 2. This lever system has five rigid elements (including the seat tube and crank), and five fulcrums (including the pedal spindle and bottom bracket). You can see that it will work identically if it is rotated to any angle around the bottom bracket so long as the relationship between all the elements is maintained, that is, there is no change in the angular range of any of the lower leg joints as the whole system is rotated. (Note that this is not the same as sliding the saddle back and forth on its rails. To do so changes saddle height.) The knee joint works exactly the same and has the same forces acting through it regardless of its orientation. As an example, note that a recumbent rider's position does not in any way relate to the force of gravity acting through the knee. The recumbent rider's legs act in the same mechanical way on the crank, even though he is rotated roughly 90 degrees from the standard position. The gravitational constraint that is lost at the saddle is replaced with a mechanical one, a seat with a backrest.
As a rider is rotated about the bottom bracket, the angle between his torso and hips may vary. There is a fundamental connection between the activity of the hip extensor muscles and the muscular torque at the knee joint, but there is no evidence of any sacrifice in propulsive power as the range of motion of the hip joint varies. Moreover, within the confines of the diamond frame, the extent to which a rider will vary his torso angle during normal cycling by changing posture and hand position surpasses the small changes that any rotation about the bottom bracket will have.
[This makes sense for any position in which the upper body is at a sufficient angle to the leg that the gluteus muscles contract and can contribute power, and in which it is not necessary to pull on the handlebars to counteract the force on the pedals. Note that the illustrations in the article show a cyclist in a racing position, with low handlebars. A bolt-upright cyclist does not enjoy these advantages -- John Allen]
It should be easy now to see that a rotation of the leg/crank lever system about the bottom bracket is the same as a change in seat tube angle. A shallow seat angle has the same effect as rotating the rider in our diagram clockwise about the bottom bracket; a steep one does the opposite. In both cases, the plumb bob will swing away from the pedal spindle, but the lever system remains the same. Obviously, too much rotation away from seat tube angles found on diamond frames will change the effects of gravity enough to be noticeable. The horizontal component of the peak pedal forces may become large enough to overcome the frictional forces that help keep you in the saddle. Some mountain bike riders used to complain about how the 69-degree seat angles on the old Ritchey-type bikes made them feel like they were always pushing themselves off the saddle. On the other hand, too steep a seat angle puts too much of the rider's weight on his arms and shoulders.
I feel that proper fit should involve more than a good seated position. A good cyclist uses a variety of riding positions, including two different out-of-the-saddle positions - one for sprinting and a slightly different one for climbing. [Well, a range of positions for climbing depending on the steepness of the climb -- John Allen]. The rider's center of gravity (CG) over the pedals changes among all three positions; good overall bike position would assure that the rider is well balanced and does not have to expend excessive muscular energy in the arms and shoulders to support his weight in any of them. Also, there may be other factors that complicate fit, including unique anatomical characteristics and poor upper body strength. None of these considerations are served at all by the KOPS method. My alternative fitting regimen outlined below considers these factors as well as the standard requirements of comfort and efficiency.
![]()
![]()
The CG of a seated rider in a fairly aerodynamic position will often be about 1 to 1.5 inches (2.5 to 3 cm) in front of the bottom bracket. I have determined this in two ways: by direct measurement of the rider's anatomy (measuring this balance point), and by weight distribution calculations (weighing the axles). Of the two, the latter is the more accurate. The result is generally consistent with a 45%/55% fore-and-aft weight distribution that many classic cycling texts regard as optimal.
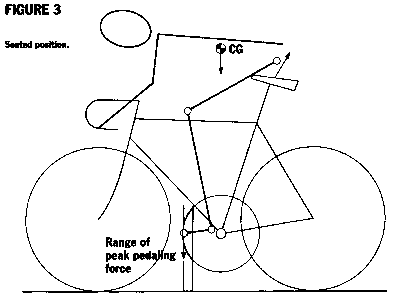
The peak pedaling force applied by the seated rider produces an upward and slightly rearward force at the saddle (Figure 3). If pedaling forces are small, the cyclist is able to remain seated because the upward component of force is smaller than the rider's weight on the saddle, and the rearward force is smaller than the static friction between the rider and the saddle. During the angular phase of the pedal cycle when the pedaling force is small, the rider tends to fall forward due to the moment between his CG and the saddle, and this must be resisted with upper body and torso effort.
As peak pedaling forces increase, the gravitational constraining forces on the rider at the saddle are no longer sufficient and larger arm and torso efforts are required to maintain a seated position. At extremely high pedaling forces, the rider comes out of the saddle to straighten the load path for his arms which allows them to effectively resist the loads created by the much stronger leg muscles. The diagram of the lever system in Figure 1 is no longer accurate at this point; the rest of the rider becomes a complicated system of levers as well.
The two basic out-of-the-saddle riding positions are useful in many circumstances. The one mentioned above is used to accelerate as rapidly as possible during a start, jump, or sprint. A slightly different position is used to climb hills. These two circumstances are worth considering in more detail in order to understand how the horizontal saddle position determines the rider's overall position on the bicycle.
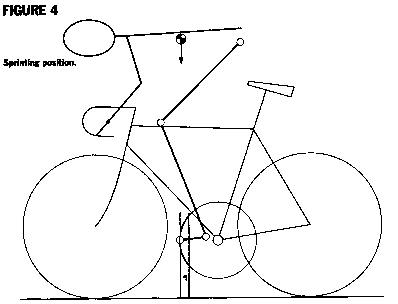
The sprinting position is the simpler of the two. The rider is making such large pedaling forces that his torso and upper body can do little more than resist the peak forces of the power stroke. The arm effects between the peaks keep the bicycle leaning in the direction that puts the pedal being pushed under the rider, as well as locating the rider and contributing a small amount to the pedal forces. Peak pedaling forces are large compared to gravitational forces, and the rider's position adjusts accordingly, shifting his upper body forward to achieve the best load path for the arms (Figure 4). The rider's CG is typically forward of the pedal at this point. During the phases of the pedal cycle when pedaling forces diminish (around the six and twelve o'clock positions), there is a small torque on the rider about the pedal. As before, this will tend to cause the rider to fall forward and will need to be resisted with upper body and torso effort.
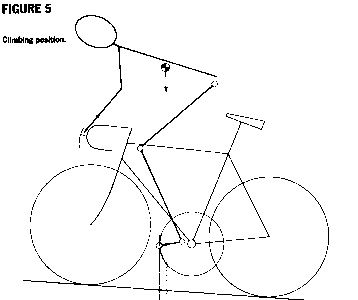
The pedaling forces are smaller when climbing. When a rider gets out of the saddle to climb (Figure 5), his CG moves over the region directly above the range of pedal positions where the pedaling forces are high (from eight to ten o'clock). This allows the rider to "balance" on the pedals when the forces are high, minimizing the arm effort required and lets the full weight of the rider contribute to pedaling forces. The torque on the rider is still there when the pedal forces decrease and must be resisted, but it is smaller because the rider's CG is closer to the bottom bracket spindle. The geometry of the link between the torso and bars made by the rider's arms when climbing out of the saddle is something I pay particular attention to when I fit a rider, but is somewhat flexible due to the larger number of bones and muscles that make it up.
With this insight into pedal forces and weight distribution for both in- and out-of-the-saddle riding, we can look at what happens to rider position as the seat angle is varied, and how these variations affect performance. We can start with something in the middle of the range of seat tube angles and see what changes occur to the rider's position as this angle is varied.
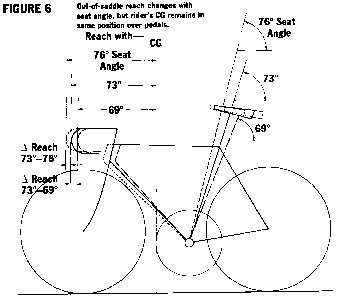
At about 73 degrees, the rider's CG is a little in front of the bottom bracket spindle when seated, and it moves a little forward when he rides out of the saddle. As the seat tube angle is rotated back (made shallower), the seated rider's CG will shift back. The bars will have to come back to keep the reach the same. However, when a rider gets out of the saddle, only the bars and pedal locations determine position. Since the bars are back, the standing rider's reach is shortened. There is less room available between the rider and the bars (Figure 6). At 69 degrees, the out-of-the-saddle reach is reduced by seven to eight percent. For a typical medium-sized bicycle, this change correlates to about a five cm reduction, a large change compared to typical stem length adjustments.
The opposite result occurs when the seat tube angle is steepened. The seated rider's CG moves forward and the distance between the bars and saddle is maintained by installing either a longer stem or a longer top tube. But as the rider stands out of the saddle, his CG will again move to the spot a little behind the nine o'clock pedal position. The result is that the rider has to reach farther forward to the bars. At 76 degrees, the out-of-the-saddle reach is increased by five to six percent and the rider will have to reach forward roughly four cm more than at 73 degrees. Again, you can appreciate that this is a fairly large change when compared to a typical stem length adjustment.
![]()
![]()
In both these extreme cases, there could be problems. If the seat tube angle is too shallow, rider CG will be well behind the position where it is comfortable and efficient for out-of-the-saddle riding. If he jumps out of the saddle for a sprint, he may hit his knees on the bars. In the climbing position, the rider may have to lean back uncomfortably far, putting extra stress on the arms and shoulders. In most cases, the rider can put just as much power in the pedals, but only at the expense of upper body comfort. As an example, early off-road designs suffered from these problems, although current frame design trends solve it.
Too steep a seat tube could cause a rider to have to reach too far for the bars when out of the saddle (a poor load path), cause the saddle to interfere with the rider's legs as the bike leans from side to side, or put his CG too far forward, increasing the load on the arms and torso to catch himself during the low-force portions of the pedaling cycle. Some production frames in the smaller sizes have these problems built in. They have steep seat angles and uncomfortably long reaches due to the geometrical constraints, such as wheelbase and toe overlap, forced upon them by 27-inch front wheels.
Now we can derive some insight into what proper seat tube angle should be. The correct seat tube angle allows correct weight distribution for both in- and out-of-the-saddle riding. The cyclist will find the handlebars in just the right position for a comfortable riding stance in all riding positions. I am neglecting the fact that the overall weight distribution of the bicycle affects the dynamics of the vehicle and may need to be considered, though that is not generally a problem with road frames.
I begin my fitting procedure by taking the standard anatomical measurements that have mechanical significance, including two leg lengths (inseam and hip socket to floor), foot length, torso length, and a measure of arm from the shoulder to the center of the hand as it clasps the handlebars. Then I determine the rider's CG. For convenience, I use his seated CG which I measure by placing the rider in a full crouch against the wall and have him back up on his feet a bit at a time until he is on the verge of toppling over. Since a human being always balances on his feet. I know his CG will be right over the balls of his feet at the moment he topples over. I measure this distance away from the wall. This becomes the horizontal coordinate for the rider's center of gravity.
With the anatomical measurements and the CG figure in hand, I am ready to design the frame. My first concern is setting the rider's out-of-the-saddle position. Invariably, a climbing rider will place his CG at a spot two to three cm behind the pedal spindle at the nine o'clock pedal position. This is the case for all riders. The reach the rider needs to the bars from this position depends on several factors, including torso and arm length, as well as how his body mass is distributed. The seated CG figure helps me here. For instance, a rider with a lot of upper body mass will not want to reach as far to the handlebars as another rider of equal stature but with more lower body mass. I have worked out a mathematical equation that establishes a good arm-to-torso relationship for a comfortable climbing position using the rider's seated CG, plus his arm and torso measurements (this relationship includes a significant amount of anatomical information that involves the relationship of numerous bones and joints in the standing rider). The math gives me the horizontal distance from the pedal at the nine o'clock position to the handlebars.
Now we know where the handlebars and pedals are, and so, using the rider's torso and arm measurements, it's a simple matter to extend the top tube back, locating the seat. At this point, I look at the overall design and consider a rider's particular requirements. For instance, if the rider demands a short wheelbase, I'll try to change the design to accommodate him.
In my experiences so far, I've found that most riders are suitably positioned with a seat angle that falls between 72 and 74 1/2 degrees. What is important is that I have not noticed any specific correlation between seat angle and my customers' femur bone length. I am reasonably certain that none exists. Still, it is easy to see how the KOPS method can get by. It usually puts the rider in the range of correct fit, although in my experience, the more anatomical proportions vary from the norm, the more off the mark the KOPS method is.
In general, I believe this new way of approaching the fit problem is physically correct. It ignores the arbitrary knee/pedal relationship of the KOPS method and replaces it with a procedure that tries to minimize the muscular efforts required by the rider to maintain each riding position. So far, I haven't had any complaints from my customers and I've been able to clear up fit problems for riders that were positioned poorly by the KOPS method.
Last updated: 7 December 1998 [Minor proofreading, comments, fixed bad links: John Allen, May 18, 2015]
![]()
![]()
![]()